Simultaneous Equations

Simultaneous equations involve at least two unknown that must be found. If we have two equations and two unknowns or three equations and three unknowns then we can generally solve the equations. Typically the two unknowns are labelledandas in the following simultaneous equations.

(1)

(2)

The procedure for solving simultaneous equations is:

1. Choose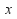or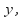and make the size of the coefficients of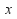or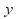the same. In the above equations the coefficients of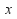are 2 and 3, and the coefficients of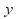are 1 and 2. We can make the coefficients of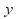the same by multiplying (1) by 2, then both equations have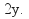The new equations are

(3)

(2)

2. We can now eliminate the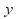terms by subtracting: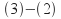gives

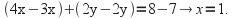
3. Now find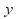by substituting this value for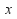back into one of the equations (1) or (2) and solve to find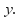

Suppose we substituteinto

Example: Solve the simultaneous equations

(4)

(5)

We can make thecoefficients the same size by multiplying (4) by 2 and multiplying (5) by 3. This will result in them being the same size but having opposite sign. We do not subtract – we add to eliminate the- terms.

(6)

(7)

(6)+(7) gives

Substituteinto (4) to obtain