The Minimum Distance Between a Point and a Line

We want to find the minimum distance between a pointand a lineIf We label the point on the line which makes this distance a minimumthe we must find the distance

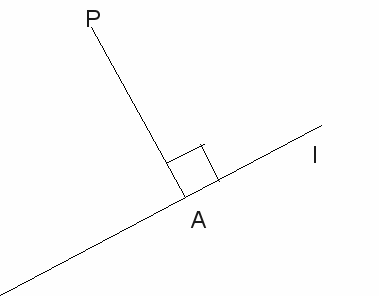
This distance will be a minimum when the lineis at a right angle toThis means that the dot product ofwith the tangent vectortoisWe can use this to find and then the distance

Supposeand the equation ofis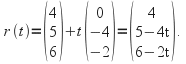

We take the pointas having coordinates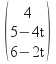so the vectoris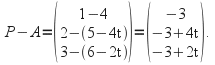

The tangent vector of the lineis

The dot product ofand the tangent vector is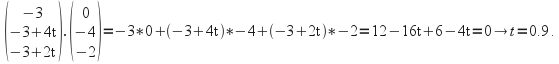

Then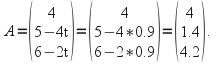