The Product of Two Binomial Expamsions

The General Binomial Expansion takes the form

Any expression of the formcan be evaluated using this expression whatever the values of A and B – negative, decimal factional or even complex numbers.

We can expand the product of two binomial expansions by finding each individual binomial expansion.

Example: Expandup to and including the term in

We expand each expression up to

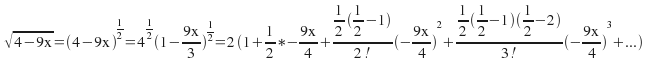
Simplifying the constant for each term gives

Simplifying the constant for each term gives

Now we multiply the binomial expansions together:

Each term in brackets can then be simplified.

The first expansion is only valid forand the second is only valid forso the product is only valid for the smallest of these two intervals: