The Point of Intersection of Two Lines in Three Dimensions

If two lines intersect, theyare both in the same place at the same time, so to speak. We don'tknow what the point is, but because they both meet at the same point,we can put the equations of the lines equal to each other. This willresult in simultaneous equations for the parameters. We solve them,then substitute back in to the lines to find the point.

Example: 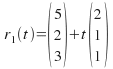and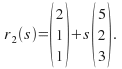Findif the lines intersect and if they do intersect, find the coordinatesof the point of intersection.

Put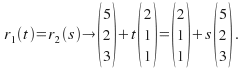

Put each component ofequalto the corresponding component ofWeobtain

(1)

(2)

(3)

(2)-(3) gives

Substituteinto(1), (2) or (3) to give t=1.

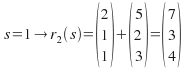and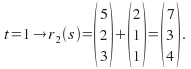

Hence both equations meet atthe same pointwhen

If the lines do notintersect at a point then the two points will not be the same orequivalently there will not be values of s ant t that satisfy allthree equations simultaneously.

Example: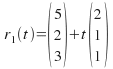and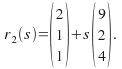

We form the same equationsas before and perform (2)-(3) to get butequation (1) is now anddonot satisfy this equation so these lines do not intersect.