Critical path analysis is algorithm that allows large projects to be planned. Each projects consists of a series of activities that must be completed. Before an activity can be started, certain other activities must be completed. The algorithm allows the ordering of activities, maybe doing several activities at the same time, so that the project is completed in the minimum time.
The table shows the activities needed to build a house with durations given in days.
|
Task |
Description |
Duration |
|---|---|---|
|
A |
Excavate foundations |
2 |
|
B |
Pour concrete |
1 |
|
C |
Build walls |
3 |
|
D |
Construct roof sections |
7 |
|
E |
Put up roof sections |
1 |
|
F |
Tile roof |
3 |
|
G |
Install plumbing |
4 |
|
H |
Install electrics |
3 |
|
I |
Install windows and doors |
2 |
|
J |
Paint ceilings |
2 |
|
K |
Paint walls |
3 |
|
L |
Lay carpets |
2 |
The first thing that we need to do is to decide which of the activities depend on other activities:
-
B requires that A be complete.
-
C requires that B be complete.
-
E requires that C and D be complete.
-
F requires that E be complete.
-
G, H, and I all require that F be complete.
-
J and K require that G, H, and I be complete.
-
L requires that J and K be complete.
With this information we can draw an activity network. In an activity network the edges represent activities, such as those listed above. The nodes represent events. An event is the start and/or finish of one or more activities. The activity network for the house building example is shown below.
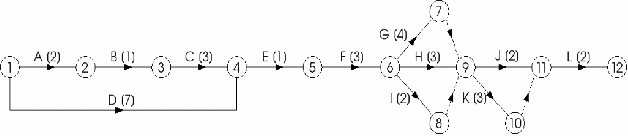
Some of the arcs do not have associated activities. They are dummies, and are shown as dotted lines eg the arcs from 7 to 9 and from 8 to 9. Dummies will be explained later. As you can see, there are a few activities that can occur simultaneously. The activity network can be used to find the critical path through the operation (finding a critical path). It is the longest path and determines the minimum length of time that is necessary to complete the house. For instance the longest path between nodes 1 and 4 is via D above, so D is a critical activity, the longest path between nodes 6 and 9 is via G so G is a critical activity. Similarly, so is K. The critical path is 1- 4 -5-6-7-9-10-11-12, where 1-4 is via activity D.
