The seven bridges of Konigsberg is a famous problem in graphtheory. The city of Konigsberg in East Prussia had seven bridgescrossing the river Pregel, some to an island, before crossing anotherbridge to the other side of the river.
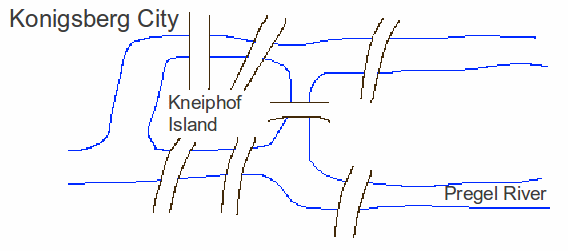
The problem is to find a route crossing each bridge exactly onceand was solved in 1736 by Leonard Euler. He redrew the map above as anetwork of arc repressing a bridge crossing and nodes representingeach piece of land, drawing a diagram similar to the one below.
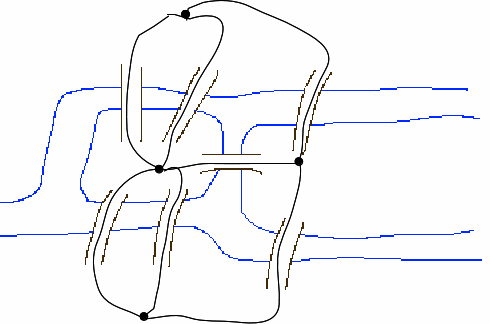
Euler observed that when a vertex is visited in while tracing thegraph, there must be an edge entering the vertex and another edgeleaving it and so the order of the vertex must be an even number. This must be true for all but at most two of the vertices - thestart and end vertices and so a connected graph is traversable if andonly if it has two vertices of odd order, unless the start and endvertices are the same in which case every vertex has even order. Thediagram above shows four vertices of odd order so the network is nottraversable and the each bridge cannot be crossed exactly once.
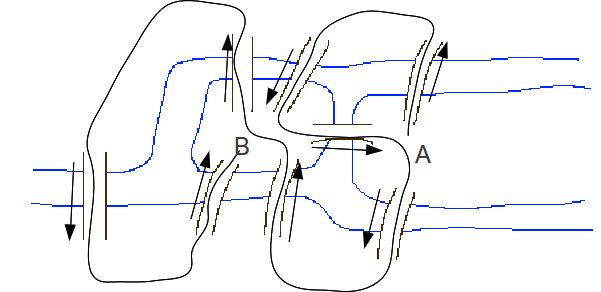
If an extra bridge is added a the network may become traversable.One solution and route is shown blow. The route starts at A and endsat B.