Proof of the Stable Solution Theorem

For a two player, zero sum game, a stable solution is one such that each player always plays the same, unchanging strategy. The Stable Solution Theorem states that there will only be a stable solution when the row maximum of the matrix representing the playoffs for one player equals the column minimum.

If the matrix represents the payoffs forof each combinations of strategies of each player, withandplayer A's and B's play safe winnings respectively, then

1. For any zero sum game,

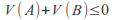
2. A zero sum game has a stable solution if and only if

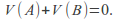
Prove 1 first. If both players play safe thenwins at leastandwins at leastso the total winnings are at leastbut in a zero sum game the total winnings are always zero so

Sinceis the row maximin there is a row in which the smallest element isIf the row is the kth row then playerwill be playing safe by playing strategySimilarlyis the column minimax, there is a column minimax, there is a column, say the lth, in which the largest entry isPlayerwill be playing safe by choosing strategy

The value of the game tois given by the elementin the matrix.sinceis the smallest number in rowandsinceis the biggest number in columnHence

buthencehenceandis then the smallest in rowand the biggest in column

Playerassumes that playerwill play strategyThere is no benefit toin changing strategy sincegives the biggest payoff toalso assumes thatwill play strategyThere is no benefit toin changing strategy sincegives the biggest payoff tosowill always play strategy l. The game is table andis the saddle point.

To prove the 'only if' part, note that if the game is stable there is a saddle point or possibly points that give the game's value. Since this is a zero sum game this must be equal and opposite for each player so