A zero sum game is one in which the total pay-offs are the same for all possible combinations of players' strategies. Each player can only gain at the expense of the other players so any player's loss is balanced by an equal gain made by other players.
It does not actually matter much whether the sum of the pay-offs is zero (the strict requirement for the zero sum game) or another number, as long as the total is the same for all possible outcomes. For this reason, zero sum games are often called constant sum games.
A real life example of a zero sum game is poker between friends. One player's loss is another's gain.
Financial markets offer many examples of zero sum games. For example the writer of an option can only gain what the holder loses and vice-versa. Although securities markets are expected to have an overall positive outcome, attempts to out-perform are zero-sum, in that all out-performance by winning investors must be balanced by out-performance by losers.
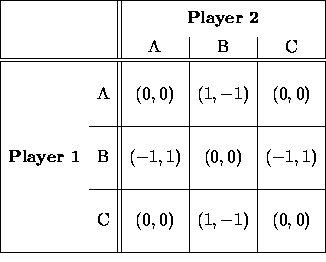
A game's payoff matrix is a convenient representation. Consider for example the two-player zero-sum game whose payoff matrix is shown above.
The order of play proceeds as follows: Player 1 chooses in secret one of the strategies
and Player 2, unaware of the Player 1's choice, chooses in secret one of the three actions
or 
Then, the choices are revealed and each player's winnings is affected according to the payoff for those choices.
The table above shows the payoff for each player for the strategies they adopt. Each player may adopt strategy
Whatever strategy is adopted by each player the sum of the payoffs is zero.