Using The Hungarian Algorithm to Find the Least Cost Allocation

The Hungarian algorithm provides a method of allocating workers to tasks, with each worker doing one tak, so that the total cost of doing all the tasks is minimized.

The steps in the algorithm are:

1. Find the reduced cost matrix.

2. Determine the minimum number of straight lines – horizontal or vertical – which will cover all the zeros in the reduced cost matrix.

3. If you cannot cover all the zeros in an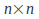matrix with fewer than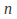lines, then you have found an optimal solution.

4. If you can cover all the zeros in an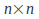matrix with fewer than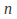lines – vertical or horizontal – the solution can be improved.

5. Draw in these lines and look for the smallest uncovered element

6. Add x to the element in each covered row and column, adding it twice to any element crossed by vertical and horizontal lines.

7. Subtract x from every element of the matrix.

8. Repeat 2 to 7 until an optimal solution is found.

For example, consider the cost matrix below, which shows the costs of workers Andrew, Boris and Charles to do tasks 1, 2 and 3.

Subtract the smallest element in each row from all the entries in that row. Subtract 12 from each element in row 1, 39 from each element in row 2 and 28 from each element in row 3 to give

Subtract the smallest element in each column from all the entries in that column. Subtract 1 from each element in column 1, 0 from each element in row 2 and 0 from each element in row 3 to give 

All the zeros in the last matrix above can be covered by two lines – a horizontal line in the second (Boris's) row and a vertical line in the third column (Task 3).

Since all the zeros can be covered by two lines, the solution is not optimal.

The solution can be improved.

The smallest uncovered element is 8.

Add 8 to each covered element (and twice to elements crossed by vertical and horizontal lines) to give the matrix

Subtract 8 from every element.

Now we need three lines to cover all the zeros, as shown.

The solution is now optimal, with Andrew doing task 3, Boris doing task 1 and Charles doing task 2. The cost is found by referring to the original cost matrix: 12+40+36=88.