The complex conjugate of a complex number
is written
and is obtained from
by changing the sign of the imaginary part of
Ifthen
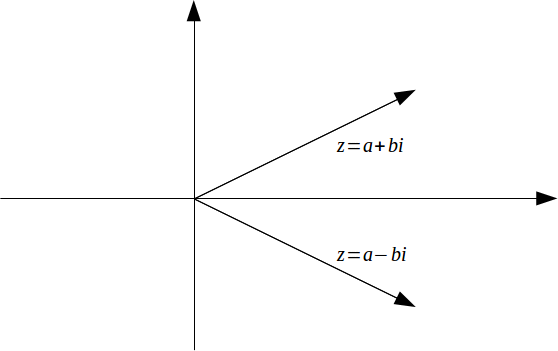
On an Argand diagram the complex conjugate ofis obtained by reflecting the pointin the real axis.
The complex conjugate has several important properties which are inhertied by the sum, product, difference and quotient of complex numbers in a natural way.
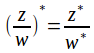
If we have the polar form of a ciomplex number,
then
In general, all we have to do to obtain the complex conjugate of a complex number is to change
into
wherever it occurs, however the number is expressed.