The Fundamental Theorem of Algebra

The Fundamental Theorem of Algebra is one of the most important theorems in algebra, maybe the most important. It states that the number of roots of a polynomial of degree is exactlyThis means also that the number of roots of the polynomial equationis alsoThis is because ifis a root thenis a factor, so that the number of factors is equal to the number of roots.

There are several points to remember:

1. The roots may be complex or real. The fundamental theorem only states the existence of the roots. It does not state their nature.

2. If all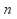roots are real then the graph of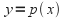will intersect the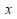– axis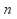times – once for each root.

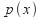3. Ifhas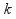roots, then it will have at least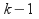turning points, because there has to be a tuning point between any two consecutive roots, and there may be other turning points, where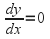besides.

There is also a very useful theorem which help to locate the roots:

If all the coefficients ofare real then ifis a complex root ofso is the complex conjugate. This often means that a polynomial can be factorised into a product of linear factors, with real but not necessarily rational roots, and quadratic factors.

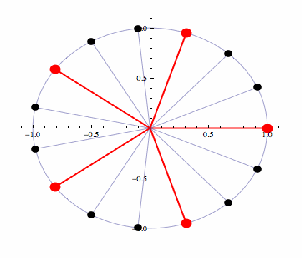
The n Roots of Unity

There is a very aesthetic illustration of the Fundamental Theorem. The equationhas n roots, which all lie evenly spaced on a unit circle at the origin when drawn on an Argand diagram. These are called theroots of unity. The diagram shows the five roots of unity in orange and the 16 roots of unity in blue. Note that 1 is always a root.