\[A(x,y)\]
in the diagram below. where \[x=y\]
.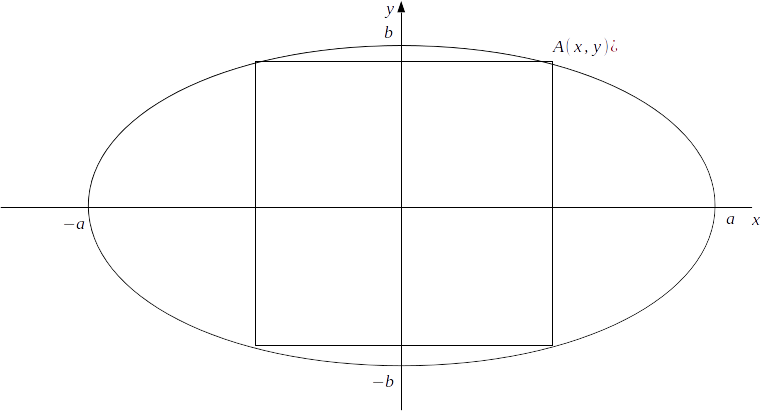
\[\frac{x^2}{a^2} + \frac{y^2}{b^2} =1\]
>If
\[x=y\]
then \[\frac{x^2}{a^2} + \frac{x^2}{b^2} =x^2 ( ( \frac{a^2+b^2}{a^2 b^2} =1 \rightarrow x = \frac{\sqrt{a^2 +b^2}}{ab}\]
>Then
\[y=\frac{\sqrt{a^2 +b^2}}{ab}\]
and the vertices of the square are at \[(\pm \frac{\sqrt{a^2 +b^2}}{ab}, \pm \frac{\sqrt{a^2 +b^2}}{ab} ) \]
