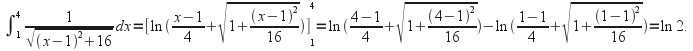Integrating Reciprocals of Square Roots of Quadratics

To evaluatewe complete the square for the quadratic expression to obtain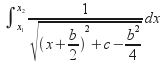then make the substitution simplify and integrate.

Example:

Complete the square to obtain

and

The integrand becomes

is a standard integral:Neverthelesscan be integrated by multiplyingby the fraction

The numerator is the differential of the denominator sinceand

To complete the integral we can either substitute back the original substitution to obtain

Now evaluate the limits