\[\int^1_0 tan^{-1} xdx\]
consider the following graph.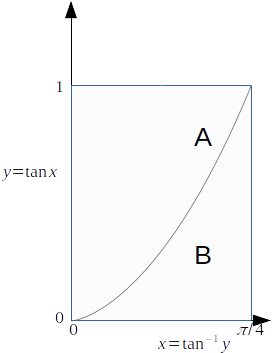
\[A+B= \frac{\pi}{4}\]
, but \[A=\int^1_0 tan^{-1} y dy, \; B=\int^{\pi /4}_0 tanxdx\]
so\[\begin{equation} \begin{aligned} \int^1_0 tan^{-1} y dy &= \frac{\pi}{4} -\int^{\pi /4}_0 tanxdx=\frac{\pi}{4} - [- ln(cosx)]^{\pi /4}_0 \\ &= \frac{\pi}{4}+ln(cos( \pi /4)) -ln(cos (0))= \frac{\pi}{4}- \frac{ln(2)}{2} \end{aligned} \end{equation}\]
