Complex Fractions
Typically we have to express a complex fraction
in the form
We do this by multiplying top and bottom by the complex conjugate of the denominator, remembering that
The complex conjugate of
Example: Express
in the form
Argand Diagrams
We may also have to plot complex numbers on an Argand diagram. This is a normal set of
axes:
is plotted as the point
In the diagram below the complex number
s plotted as the point
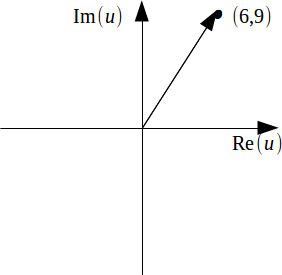
Magnitudes, Arguments and the Polar Form of Complex Numbers
The magnitude of
the argument of
The polar form of
is written as
Multiplying Complex Numbers
Given two complex numbers
and
we can find the product
We can express this in polar form as above,
then
Or we can expressand
in polar form then using the normal rules for multiplying exponentials:
so
Dividing Complex numbers
We can use the method of the top of the page to express in cartesian form, or, if we require polar form, using the normal rule for dividing exponentials:
