The differential equations
is separable We can write this equation as
Integrating both sides gives
where
Some first order differential equations are not separable. Often the most suitable way to solve it is the integrating factor method, which can be used to solve equations of the form
If we multiply both sides by the integrating factor,
the equation becomes
we can write this as
Integrating gives
and dividing by
gives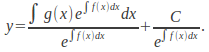
The constant
can be found to solve the initial differential equation if we have simultaneous values of
and
(if we don't have these then we just incliude the integrating constant C – this is the feneral solution).
Example: Solve the differential equation
if
so
Multiply by the integrating factor to give
which we can write as
We can integrate this. Obtaining
then dividing bygives
when
so
then the solution is