Many systems of simultaneous equations have determinants and these are reflected in the matrices of coefficients. Sometimes the determinants of the matrices can be factorised by considering the symmetries of the rows (or columns).
Example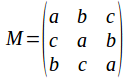
Obviously there is symmetry among the rows and if a, b and c are equal the determinant is zero. This might lead us to think that the determinant includes factors of the form
If
then
This gives us the matrix
with determinant
Then a=0, -c or c.
We may be better to consider consider the third row as the sum of the first two. This gives
and
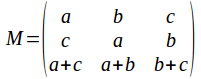
Since the third row is the sum of the first two the determinant is zero.
The determinant must be
The determinant of the original matrix is +1 and so is the coefficient of (1) so
and thedeterminant is