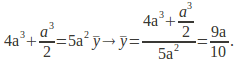We can find the distance of the centre of gravity from a line of a point by taking moments about the point for each part of the lamina. We equate this to the moment of the lamina as a whole and solve the equation to find the distance of the centre of gravity from the axis.
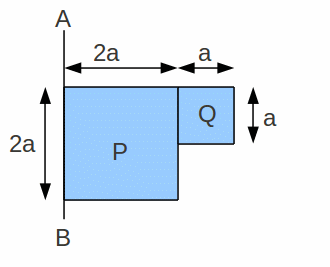
The lamina below has uniform density, so the centre of gravity of P is at the centre of P and the centre of gravity of Q is at the centre of Q.
Taking moments about AB, we can draw up the table:
|
Section |
Distance of centre of gravity from AB |
Area |
Distance * Area |
|
P |
|
|
|
|
Q |
|
|
|
|
Lamina |
|
|
|
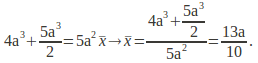
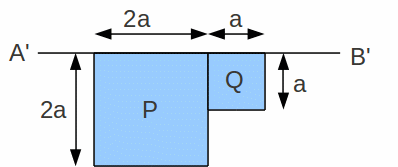
Taking moments about A'B':
|
Section |
Distance of centre of gravity from A'B' |
Area |
Distance * Area |
|
P |
|
|
|
|
Q |
|
|
|
|
Lamina |
|
|
|