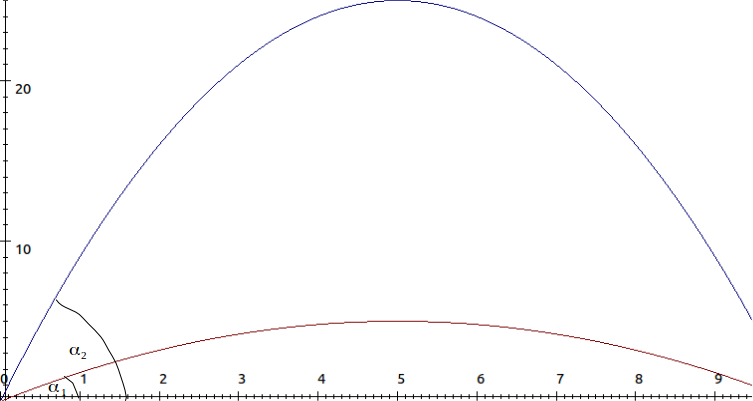
\[\alpha_1 , \alpha_2\]
respectively.
The cartesian equation of projectile motion is \[y=x \tan \alpha - \frac{gx^2}{2 u^2}(1+ \tan^2 \alpha )\]
.When
\[y=0 \]
, \[0=x \tan \alpha - \frac{gx^2}{2 u^2}(1+ \tan^2 \alpha ) \rightarrow \frac{gx^2}{2u^2} \tan^2 \alpha -x \tan \alpha + \frac{gx^2}{2u^2}=0\]
.Hence
\[\tan \alpha_1 =\frac{x + sqrt{ x^2 - 4(gx^2/2u^2)(gx^2/2u^2)}}{gx^2/u^2}\]
\[\tan \alpha_2 =\frac{x - sqrt{ x^2 - 4(gx^2/2u^2)(gx^2/2u^2)}}{gx^2/u^2}\]
Then
\[\begin{equation} \begin{aligned} \tan \alpha_1 \tan \alpha_2 &=(\frac{x + sqrt{ x^2 - 4(gx^2/2u^2)(gx^2/2u^2)}}{gx^2/2u^2})(\frac{x - sqrt{ x^2 - 4(gx^2/2u^2)(gx^2/2u^2)}}{gx^2/2u^2}) \\ &= \frac{x^2 -(x^2 - 4(gx^2/2u^2)(gx^2/2u^2))}{g^2 x^2/u^4} =1 \end{aligned} \end{equation}\]
Hence
\[\tan \alpha_1 \tan \alpha_2 =1 \alpha_1 + \alpha_2 = \frac{\pi}{2}\]
