One of the basic equations of physics is
or
If the work is done in a time
then we can divide both sides byto obtain
or
where
and
We can generalise this equation: If a body is travelling at a velocity
against a force
then the power needed to overcome the force is
It should be noted that at any instant the body may be accelerating or decelerating, so that v is an instantaneous, not necessarily a constant, speed. If a force is applied greater than the force needed to over come the resistive forcethen the body may accelerate, or the potential energy of the body may increase in some way. Given a power
and a velocitywe may find the driving force also using
Example
A lorry of mass 1500 kg moves along a straight horizontal road. The resistance to the motion of the
lorry has magnitude 750 N and the lorry’s engine is working at a rate of 36 kW.
a) Find the acceleration of the lorry when its speed is 20 m/s.
The lorry comes to a hill inclined at an angle
to the horizontal, where
The magnitude of the resistance to motion from non-gravitational forces remains 750 N.
The lorry moves up the hill at a constant speed of 20 m/s.
b) Find the rate at which the lorry's engine is now working.
a)
The resultant force=1800-750=1050N
Now use
for the lorry – note thathere is the resultant force and not the 750N force in the question.
b) The lorry does work to overcome the force of friction and to increase the gravitational potenital energy by travelling up the hill.
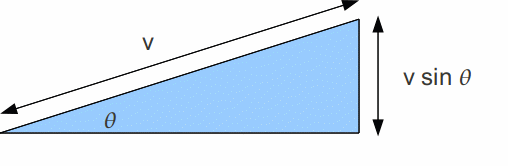
In 1 second the lorry travels a distance v up the hill so from the diagram above, rises a vertical distance
