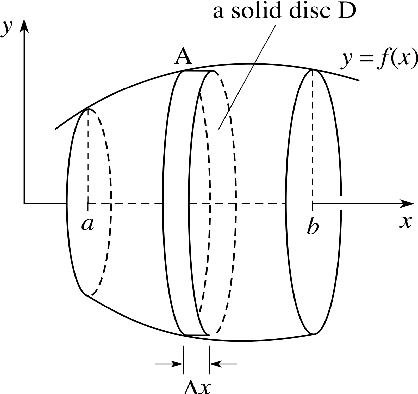
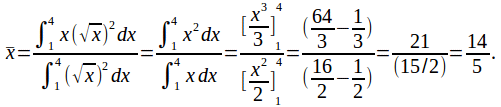When a curve
is rotated about the
- axis, the centre of mass of the solid generated will line on the– axis because of the symmetry of the curve. The centre of mass will not lie on the
– axis however.
If the centre of gravity of a volume of revolution of mass
is at
then taking moments about the- axis for the section of solid of thickness
of radiusgives a mass for this section of
so letting
integrating and equating to the moment of the whole solid gives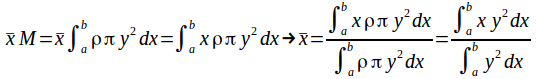
Similarly the centre of mass of the solid of revolution for a curve
rotated about the- axis is
where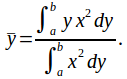
Example: Find the centre of gravity of the solid of revolution formed by
between
and
