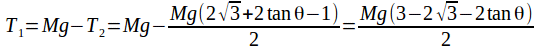In general for a system to be in equilibrium, the forces must balance in each direction, and the moments about any point must sum to zero.
When a lamina is suspended by two inelastic strings, we can find the tensions in the strings by resolving vertically and taking moments about a point where one of the strings is attached to the lamina.
The equilateral triangle of mass in the form of a lamina of mass
below is attached to two strings, one a quarter of a side from a vertex and the other at a vertex, so that the topmost side AB is at an angle
to the horizontal.
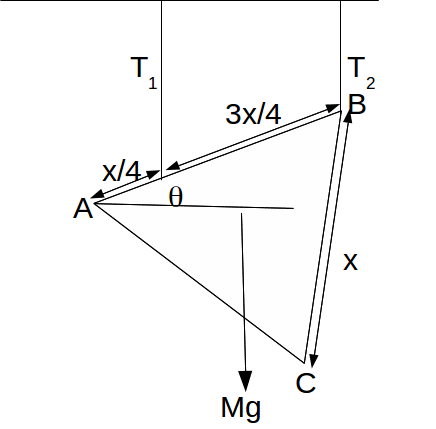
The centre of gravity O is two thirds of the distance from A to the midpoint of the side BC, and and the line from A to the midpoint of BC bisects the angle A so makes an angle
with AB and an angle
with the horizontal.
Resolving vertically for the lamina gives
(1)
Taking moments about A gives
which simplifies to
(2)
(2)-(1) gives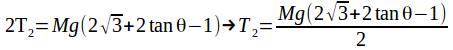
then