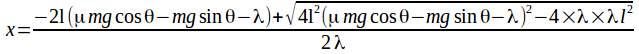When a particle is attached to a an elastic string on a rough plane, it will come to rest at a point on the slope where whatever gravitational potential energy the particle started with has been turned into elastic potential energy in the string of been used to overcome friction.
The particle below is attached to an elastic string at a point A.
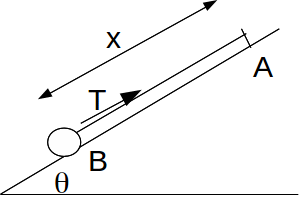
Suppose we take the gravitational potential energy at A as being zero, then at B the particle has gravitational potential energy equal to
If the particle is released from rest at A, then the initial kinetic energy is zero and the initial elastic potential energy is also zero because the string is not stretched.
The total initial energy is then zero.
If the coefficient of friction is
then the friction force
The work done against friction in moving from A to B is then
Conservation of energy then gives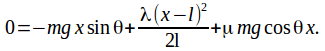
Expanding the brackets and collecting like terms gives
The solutions to this are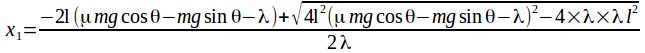
and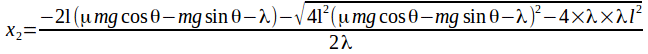
We have taken x as positive down the slope so must take the positive square root. The solution is
