Suppose we suspend a particle of mass m from an elastic spring. The tension in the string is
The particle will be in equilibrium when the tension is equal to the weight.
We have
where x-e labels the equilibrium extension.
If the particle is pulled down a further small distance
so that
the resultant force on the particle will be upwards and is given by
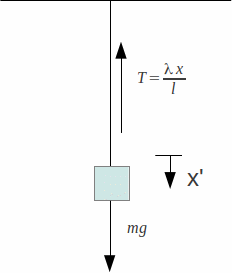
We are taking downwards as positive (since
is assumed positive), but the acceleration will be upwards and negative. Applying
gives
But
Differentiating this twice gives
so
This is the equation of simple harmonic motion
with