The Compound Pendulum

The simple pendulum models a massswinging on a rigid rod of zero mass. In practice of course the mass of the rod is not zero. The compound pendulum takes the non – zero mass of the rod into account.

A compound pendulum consists of a mass( here I will assume it to be a circular disc) attached to the end of a rod of lengthand massThe rod is hung and the rod plus mass is allowed to swing in a vertical plane.

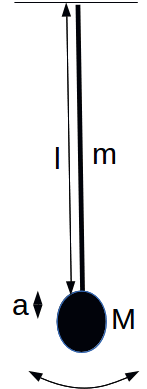
The moment of inertia of the rod about its centre is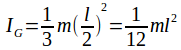so the moment of inertia about the pivot at the top is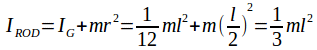

The moment of inertia of the disc about its centre isso the moment of inertia of the disc about the pivotfrom the centre of the disc is

The moment of inertia of the pendulum is then

Now the pendulum can be modelled as a particle with moment of inertiafree to rotate in the vertical plane. If it is displaced an angleto one side it will experience a restoring torque towards the vertical due to the massofand due to the rod ofso the total restoring torque isand this will be equal to the the neagive of the product ofand angular accelerationThe negative indicatesandare in the opposite sense.

Ifis small,and writing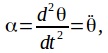

Which becomes

where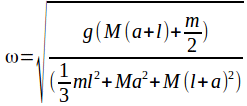

The compound pendulum will execute simple harmonic motion.

We can check the formula by puttingthen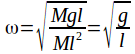just as for a simple pendulum.