Every probability distribution has a probability density function, in terms of which it is usually defined. The probability density function for the normal distribution is![]() for the uniform distribution it is
for the uniform distribution it is![]() for values between
for values between![]() and
and![]() and zero outside this interval. Both of these examples are continuous distributions, where any value in an interval may occur, though there are many examples of normal and uniform discrete distributions. The example below is for a continuous distribution over the interval 0 <=x <=3.
and zero outside this interval. Both of these examples are continuous distributions, where any value in an interval may occur, though there are many examples of normal and uniform discrete distributions. The example below is for a continuous distribution over the interval 0 <=x <=3.
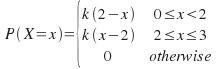
Given the pdf we can find![]()
![]()
![]()
![]() To evaluate this expression we find
To evaluate this expression we find![]()
![]()
Hence![]() to 3 dp.
to 3 dp.
The expression for the variance![]() is fundamental in higher mathematics and physics, especially quantum physics.
is fundamental in higher mathematics and physics, especially quantum physics.
These expressions are also useful for any continuous distribution defined on an interval![]()
![]()
![]()
![]()
