Apparatus:
Dynamics trolley, runway, clamp stand etc., 2 x metre rulers, top-pan balance, set-square & stop-clock.
Diagram:
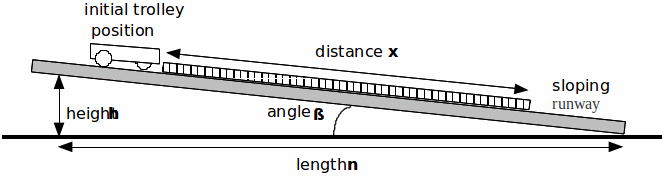
Procedure:
1. Clamp the runway in such a way that the dynamics trolley takes time,
to roll, from rest, distance
down the runway.
2. Measure this time,
three times. Calculate the average value of t.
3. In order to determine the angle of slope of the runway
measure height
and length
Length
should be at least 70 cm. Calculate
4. Calculate the acceleration
f the trolley by using
(If the trolley starts from rest, then
).
5. Repeat for four more different angles
with the timevarying between about 1 and 5 seconds.
6. Tabulate your results.
7. Measure the mass M of the dynamics trolley.
8. Plot a graph of acceleration a (in m/s 2 ) against
Ensure that your acceleration scale goes down to at least minus 0.2 m/s 2 .
Draw a best fit curve. Your graph should gently curve with a negative intercept on the acceleration axis.
9. Use your graph to find the angleof the runway when it is "frictionless" (i.e. when the acceleration of the trolley would be zero).
10. Draw a tangent to your line at the point where the acceleration is zero. Calculate the gradient
of this tangent.
11. Record the value of the intercept
on the acceleration axis.
12. Calculate the frictional force,
acting on the trolley at low accelerations given that:
13. Why is the above method of measuring anglebetter than using a protractor?