Apparatus:
Metre rule, G-clamp, stop watch, set of masses (4 x 100g), sellotape and scissors.
Diagram:
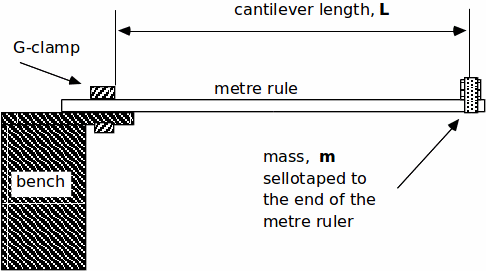
Procedure:
1. Use the apparatus, set up as shown in the diagram. Start with a length
of 0.900m (90.0cm).
2. Use a stop-watch to measure the time taken for 10 complete oscillations. However, if the total time is less than 10 seconds you should use more than 10 oscillations.
Repeat twice more to obtain two more values.
3. Use your readings to find the average time taken,
for one oscillation.
4. Repeat the above for five more different values of
5. Tabulate your results and include two extra columns showing the logarithms of bothand
You should label these columns as
and
(in cm).
Note it does not matter which 'log' button you use ('ln' or 'lg') as long as you always use the same one. Do not worry if some of the log values are negative.
6. Plot a graph ofagainst
It should be a straight line.
7. Measure the gradient, m of your graph.
8. The period of a cantilever is expected to be given by an equation of form
where
that depends on the other physical properties of the set up (e.g. the mass of the ruler). The values of
and the power
can be found by the method you have used (see full theory below). Read the theory below and state what value you have found for
Theory:
Taking logs on both sides of the equation yields:
This has the form of
where the gradient
and the intercept