The mass of every stable nucleus is less than the the combined masses of the nuclei of which they are made. The nucleus is said to have a mass defect. It cannot break up into free protons and neutrons because it lacks the mass needed to make those particles. We may think of the mass defect – more accurately, the binding energy per nucleon - as being responsible for the stability of these nuclei. The mass defect is always very small – less that 1% - of the mass of the atom. We may express it it terms of the atomic mass unit:
One atomic mass unit (u) equals one twelfth the mass of a
atom, including the mass of the six electrons:
We must be so precise since the masses we use to calculate the mass defect are so similar.
Example Calculate the mass defect of a
nucleus
The Mass Defect is given by
The Binding Energy is given by
The binding energy per nucleon increases for very small atoms and decreases for very large atoms. The peak is for iron.
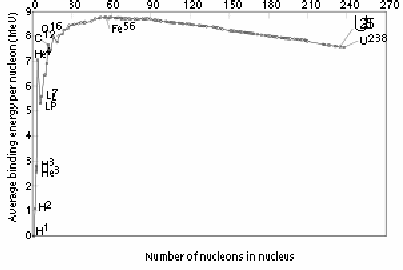
The graph implies that for small atoms the binding energy per nucleon can increase, so small atoms can become more stable if they combine into larger atoms, but that for very large atoms, the binding energy per nucleon can increase if they split up into smaller atoms. There is a peak for iron, implying that iron is among the most stable of nuclei, which is in fact the case.