An aperture of any shape can form a diffraction pattern. The diffraction pattern formed by a circular aperture is of particular interest because of it's role in limiting how well an optical instrument can resolve fine detail. In principle we could find the intensity at any point in the diffration pattern by dividing the area of the aperture into small elements, finding the wave amplitude at phase at each element and then integrating over the aperture area to find the resulting amplitude and intensity at the point in question. In practice this is very time consuming.
The diffraction pattern formed by a singular aperture consists of a central bright spot surrounded by a series of bright and dark rings as shown below.
We can describe the pattern in terms of the angle
representing the angular radius of each bright ring subtended at the aperture.
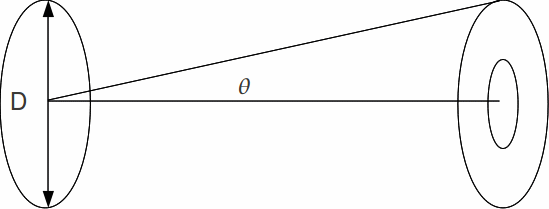
If the aperture diameter is
and the wavelength of light is
then the angular radii of maxima and minima are given by
|
Maxima |
Minima |
|
|
|
|
|
|
|
|
|
The central bright spot is called the Airy disk.
When we form an image of an object, in fact we obtain a diffraction pattern. The criterion for just being able to resolve two point objects is that the centre of one diffraction pattern falls on the first minimum of the other – the Raleigh criterion - as shown below.
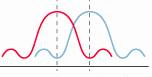
In this case the angular separation of the image centres is given by