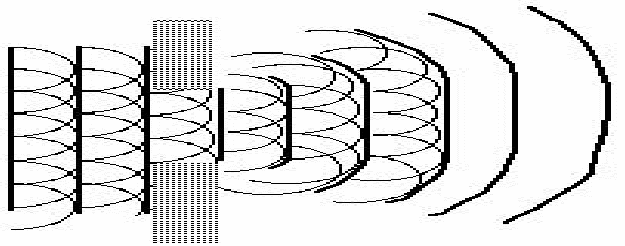
Huygen's principle eases the analysis of many problems in optics. It states:
Every point on a wavefront can be considered as a point wavesources, from which waves spread out as wavelets that move at the same speed as the wavefront. The sum of the displacements of these wavelets at a point is the displacement of the wavefront and the wavefront is a tangent to the wavelets at the point where they meet. As the wavelets move, the sum of their displacements remains is equal to the displacement of the wavefront at each point.
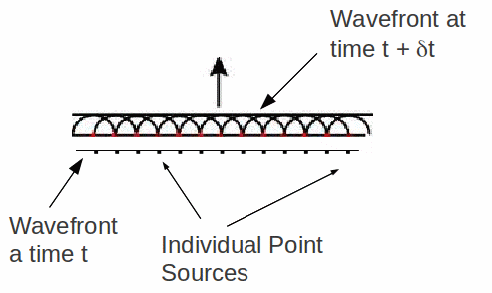
Huygen's principle can be used to deduce that laws of reflection and refraction, and explains the shape of waves that are diffracted as they pass through an opening or around an obstacle. Points that give ris to the wavelets are truncated at the edges of the opening below, while those wavelets at the edge spread out as they pass through the opening, and those in the centre of the wavefront act as they would had no gap been there.