Systems highly sensitive to initial conditions display what is called the butterfly effect, which leaves open the possibility that a butterfly flapping it's wings on one side of the world can cause a hurricane on the other side some time latter, because the flapping of it's wings can set of a series of events. This means that the long term behaviour of chaotic systems is impossible, because a difference in initial conditions of any size can lead to events of any size at some point in the future. This initial event can be so small as to be unmeasurable, maybe within the margin of error or within the rounding error of numerical calculation. This happens even though these systems are deterministic, meaning that their future behaviour is fully determined by their initial conditions, with no element of randomness.
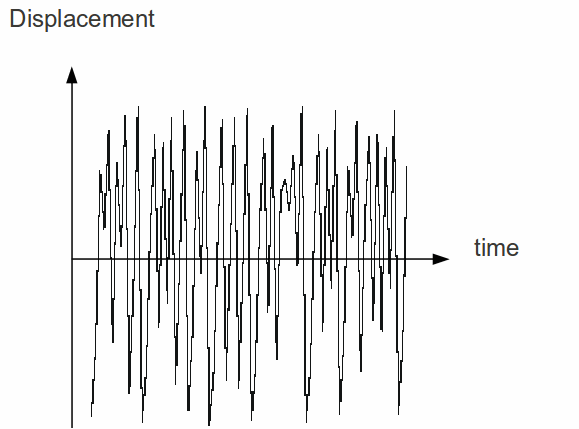
Oscillatory systems can also display chaotic motion if subject to a forcing term of certain frequencies. For example a pendulum which normally swings backwards and forwards at it's natural frequency, but if the fixed point is made to move up or down or backwards at certain frequencies, chaotic motion results. The pendulum moves around in a small space determined by movement of the fixed point and the length of the pendulum, but the pendulum never follows the same path twice. This is illustrated below.