Fizeau's rotating wheel experiment was first performed in 1849, and was the first experiment to measure the speed of light that did not require any but terrestrial observations. The apparatus is shown below. Light from a source is focused onto a rotating toothed wheel by reflection from a glass slide. Light passes through a gap between the teeth of the wheel. The reflected light is focused by mirrors 
and
onto a mirror M, then back onto the toothed wheel. The speed of rotation of the wheel is adjusted so that the time for the light to pass from the wheel to M and back is the same as the time taken for a tooth to move into the gap through which the light passed.
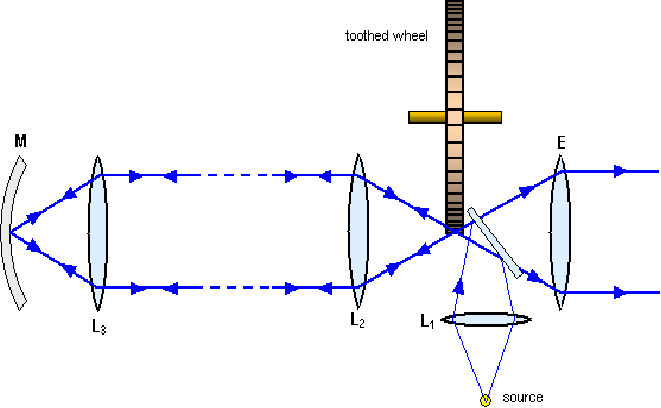
If the distance from the wheel to M is
then in the time taken for a tooth to move into the gap, the light has travelled a distance
If the wheel has
teeth, radius
and is rotating at
revolutions per second, then the tooth has travelled a fraction
of the circumference of the wheel at a speed of
so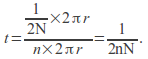
Using
for light gives
Fizeau used
giving