Suppose we have two waves of equal amplitude
but slightly different frequencies
and
Wave 1 has a displacement as a function of time given by
Wave 2 has a displacement as a function of time given by
Then
Use the identity
to write the sum of sines as a product. We obtain
This is of the form
where
The intensity of each wave is
but the intensity of the wave resulting from the interference of the two waves is
When
there is constructive interference and the amplitude of the resulting wave will be a maximum.
When
there is destructive interference and the amplitude of the resulting wave will be zero.
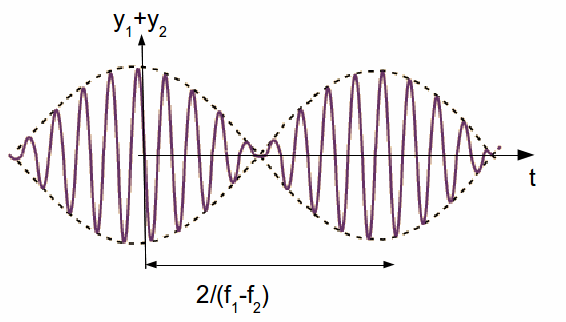
The sum of the waves is shown below as a function of time. Notice that within the wave there is a rapidly oscillating wave. The frequency of this wave will be the sum of the frequencies of the two waves.
