Continuous Probability Distributions

If a random variablehas a continuous probability distribution, thenmay take any value in an interval. The end points of the interval may be included or not. Ifdenotes possible values of the random variablethen

means 'may take values greater thanbut less than'

means 'may take values greater than or equal tobut less than'

means 'can take any real value'

Whatever the interval, all probability distributions have in common that they all integrate to one over the set of values that x may take. We can use this in problem solving.

Suppose it is known that a random valiabletakes a Triangular distribution:

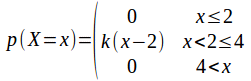
We can findby solving the equation

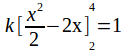
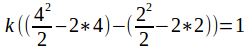
Then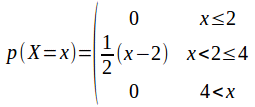

The graph ofis sketched below. The hollow circle atindicates thatis not a possible value for