Every probability distribution has a probability density function, or probability mass function in the case of a discrete distribution, in terms of which it is usually defined. The probability density function for the normal distribution is
for the uniform distribution it is
for values between
and
and zero outside this interval. Both of these examples are continuous distributions, where any value in an interval may occur, though there are many examples of normal and uniform discrete distributions. Some distributions are defined by the values they take over an interval, either one by one in the case of a discrete distribution, or in terms of a function, for either continuous or discrete distributions. For example:
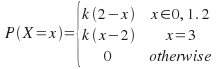
Given the pdf we can find
To evaluate this expression we find
Hence
The expression for the variance
is fundamental in higher mathematics and physics, especially quantum physics.
