When events occur at a constant average rate, the distribution decribing the events can be modelled by a Poisson distrubtion. Examples include:
Plane crashes
Spelling or grammatical errors in a textbook
School shootings (only in America)
It is important that the events occur at a constant average rate. If the rate at which events occur is not constant – because planes are getting safer, so crash less often, or spelling and grammar checkers reduce the rate at which such mistakes occur, or american students are turning away from guns – then these events cannot be modelled using a Poisson distribution, or at least cannot be modelled using a rate which is always constant.
If events occur at an average rate of
per time period or page or similar then the probability of observing x events – plane crashes, spelling/grammatical errors or school shootings – is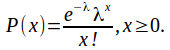
Intuitively, the expected number of events in each time period is %lambda . The variance is also %lambda If we have data for a series of events, the equality of mean and variabce may be used as evidence that the distribution is Poisson.
Because the number of events occuring in each time period (or page) is a whole number, the Poisson distribution is necessarily discrete. Poisson distributions are shown below for various values of
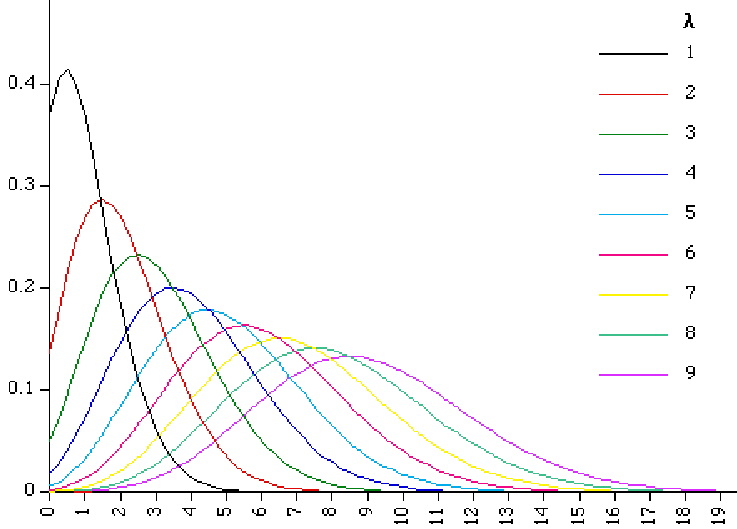
Though all the %lambda in the diagram above are integers, it is not necessary for %lambda to be an integer.