Tree Diagrams
At each stage the probability of that sequence of events equals the multiple of the probabilities.
At each stage all the probabilities add up to 1.
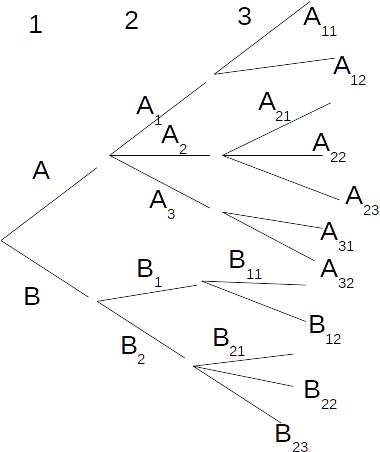
\[P(A)+P(B)=1\]
\[1=P(A, A_1)+P(A, A_2)+P(A, A_3)+P(B,B_1)+P(B,B_2)\]
\[\begin{equation} \begin{aligned} 1 &= P(A, A_1, A_{11})+P(A, A_1, A_{12})+P(A, A_2, A_{21}) \\ &+ P(A, A_2, A_{22})+P(A, A_2, A_{23})+P(A, A_3, A_{21}) \\ &+P(A, A_3, A_{32})+P(B, B_1, B_{11})+P(B, B_1, B_{12})+P(B, B_2, B_{21}) \\ &+ P(B, B_2, B_{22})+P(B, B_2, B_{23}) \end{aligned} \end{equation}\]
\[P(A, A_1, A_{11})=P(A)P(A_1)P(A_{11})\]
\[P(A, A_1, A_{12})=P(A)P(A_1)P(A_{12})\]
\[P(A, A_2, A_{21})=P(A)P(A_2)P(A_{21})\]
\[P(A, A_2, A_{22})=P(A)P(A_2)P(A_{22})\]
\[P(A, A_2, A_{23})=P(A)P(A_2)P(A_{23})\]
\[P(B, B_1, B_{11})=P(B)P(B_1)P(B_{11})\]
\[P(B, B_1, B_{12})=P(B)P(B_1)P(B_{12})\]
\[P(B, B_2, B_{21})=P(B)P(B_2)P(B_{21})\]
\[P(B, B_2, B_{22})=P(B)P(B_2)P(B_{22})\]
\[P(B, B_2, B_{23})=P(B)P(B_2)P(B_{23})\]
