Let the probability that B hits the target be
\[x\]
, then the probability that A hits the target is \[2x\]
.Since A and B aim independently the probability they both hit the target is
\[x \times 2x=2x^2\]
.
The probability that A but not B hits the target is \[2x-2x^2\]
.The probability that B but not A hits the target is
\[x-2x^2\]
.The Venn diagram is shown below.
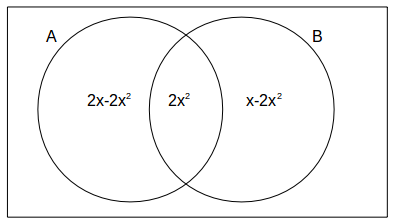
\[(2x-2x^2)+2x^2+(x-2x^2)=\frac{1}{2} \rightarrow 4x^2-6x+1=0\]
.The solution is
\[x= \frac{6 \pm \sqrt{6"-4 \times 4 \times 1}}{2 \times 4}=\frac{3 \pm \sqrt{5}}{4}\]
.\[x \lt 1\]
so \[\frac{3- \sqrt{5}}{4}\]
. 