Planes do fly straight ahead. The wind blows and the world turns and the pilot has to take account of these when he plots a course. Even with modern gps systems, , it is useful to the pilot to take account of these because of the resulting decrease in fuel use. It is worse though for the sailor, who has to take the tide into account as well
We can deal with these problems by representing the velocities of the wind, tide and boat as vectors, then using trigonometry to find the course to take.
For example:
A boat travels in a straight line across a river which flows at 3m/s between straight parallel banks 200m apart. The boat, which has a top speed of 6m/s in still water, travels directly from a point A on one bank to a point B on the opposite bank, 150m downstream of A, on the opposite bank. Assuming that the boat is moving at top speed, find, to the nearest second, the time it takes to get from A to B.
What is the first thing you do? DRAW A DIAGRAM!!
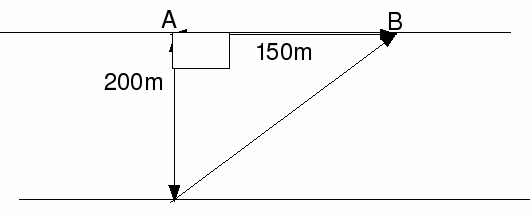
The boat has to steer a course of
The river is flowing downstream to the right at 3m/s. We don't know the direction in which the boat will steer but we do know the bearing of B from the start point is 36.87 degrees hence the angle BA makes with the bank is
We can draw the following diagram:
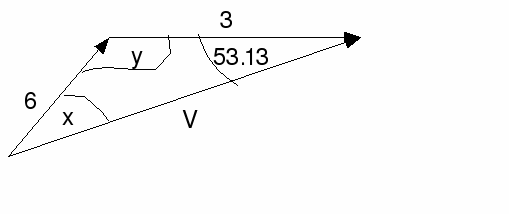
We need to calculate V, the resultant velocity. Using the sine rule we can find x:
Then
Use the cosine rule to find
The time to reach B is