Trigonometry Problem With Scaling

Suppose we have the problem below, in which it is required to find the angle

\[x\]

.

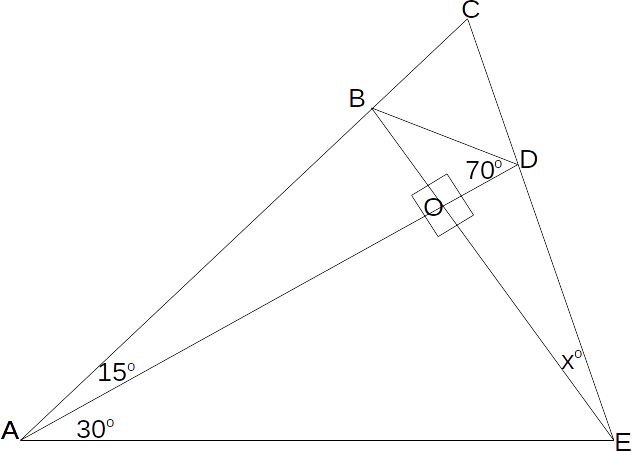
advanced trigonometry problem 1

Put as much information on the diagram as possible. If we scale the diagram, all the angles will remain the same. Scale the diagram so that

\[AO=1\]

.

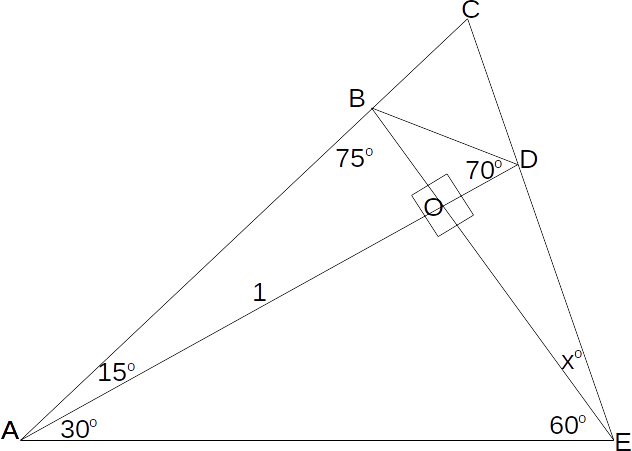
advanced trigonometry problem 2

Now we can use some trigonometry. Use the Sine Rule to calculate

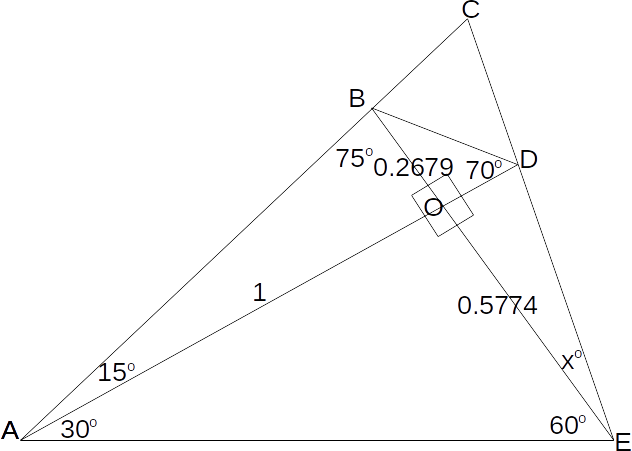
\[OB\]

and

\[OE\]

.

\[\frac{OC}{sin30}=\frac{1}{sin60} \rightarrow OC=\frac{sin30}{sin60} \times 1 =0.5774\]

\[\frac{OB}{sin15}=\frac{1}{sin75} \rightarrow OB=\frac{sin15}{sin75} \times 1 =0.2679\]

advanced trigonometry problem 3

Then

\[tan70=\frac{OB}{OD} \rightarrow OD=\frac{OB}{tan70}=0.0975\]

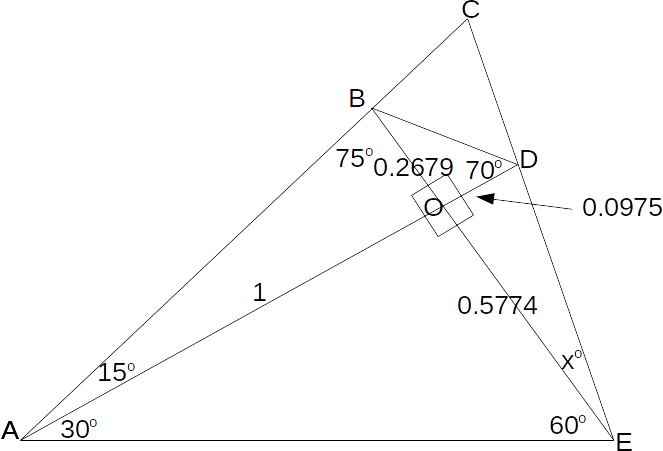
advanced trigonometry problem 4

Finally

\[tanx=\frac{OD}{OC}=\frac{0/0975}{02679}=0/1689 \rightarrow x=tan^{-1}(0.1689)=9.59^o\]

to 3 significant figures.
Note that all the working is to 4 significant figures, and the final answer to to 1 less significant figure.