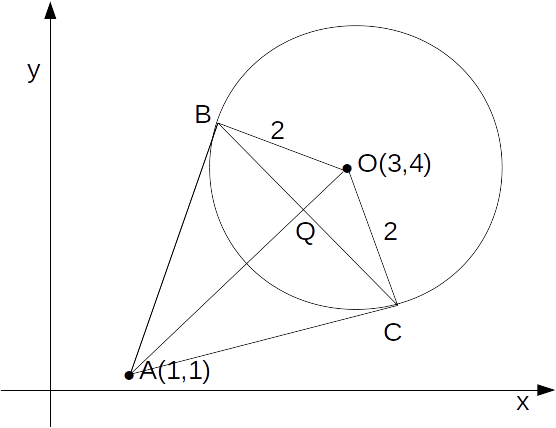
\[A= \frac{1}{2}( AO \times BC)\]
\[BC= \sqrt{(3-1)^2+(4-1)^2}= \sqrt{13}\]
.To find the other diagonal we use that triangles ABC and BQO are similar triangles, so
\[\frac{BQ}{BO}=\frac{AB}{AO}\]
.\[AB=\sqrt{AO^2-BO^2}= \sqrt{13-2^2}=3\]
, then \[\frac{BQ}{BO}=\frac{AB}{AO} \rightarrow BQ= \frac{AB}{AO} BO=\frac{3}{\sqrt{13}} \times 2 = \frac{6}{\sqrt{13}}\]
.Then
\[BC=\frac{12}{\sqrt{13}}\]
.The area of the kite is
\[\frac{1}{2} \times \sqrt{13} \times \frac{12}{\sqrt{13}}=6\]
. 