Problem Solving 2

More advanced problem solving questions involve simultaneous equations or quadratics.

Example: The height of a rectangle is 2 cm longer than the base. If the area is 48 cm2 find the length of the base.

If the base isthe height is

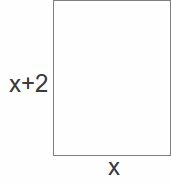
The area isand equating this to 48 givesExpanding the brackets and subtracting 48 gives

We can factorise this expression to giveEquating each factor to 0 gives

We cannot have a negative length soThis leaves

Example: Two pens and three pencils cost 57 pence. 1 pen and four pencils cost 51 pence. Find the cost of a pen and the cost of a pencil.

Letbe the cost of a pen andbe the cost of a pencil. The first sentence gives

(1)

The second sentence gives

(2)

(1)-2*(2)

Substitute into (2)