We can use the relationships between the velocities in two different frames of reference to work out measurements in one frame of reference given measurements in the other. The equations that do this without taking the theory of relativity into account are collectively called the Galilean transformation.
We consider two frames of reference S and S' in uniform relative motion. Relative to S, frame S' moves to the right with speed
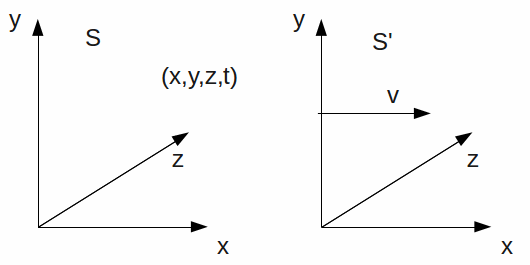
In reference frame S, the event E has coordinates
Since relative motion is along the
axis, the
and
coordinates will bill the same in both coordinate systems:
Velocities too transform in the same way:
And accelerations:
If two frames of reference are moving in the same direction with the same speed then any event will appear to be simultaneous in both frames of reference. This is experience in the train station, when it can be hard to perceive whether the train next to you is moving forward, or your own train is moving backwards.