Suppose two inertial frames
\[S, \: S'\]
coide at \[t=0\]
, with moving at constant speed \[v\]
along the \[x\]
axis of \[S'\]
.
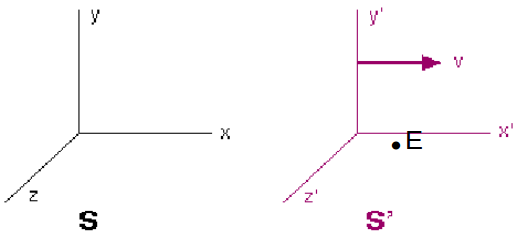
In the inertial frame
\[S\]
, an event \[E_1\]
occurs at coordinates \[(x, y, z, t)\]
according to an observer at the origin of \[S'\]
.An observer at the origin of
\[S'\]
will measure the coordinates of \[E_1\]
to be \[(x'.y',z',t')=(\frac{x-vt}{\sqrt{1-v^2/c^2}}), y, z, \frac{t-vx/c^2}{\sqrt{1-v^2/c^2}})\]
.The transformation is symmetric, so
\[(x.y,z,t)=(\frac{x'+vt'}{\sqrt{1-v^2/c^2}}), y', z', \frac{t'+vx'/c^2}{\sqrt{1-v^2/c^2}})\]
.
The Lorentz Transformation supercedes the Galilean Transformation, which is only accurate in the limit of low speeds.
