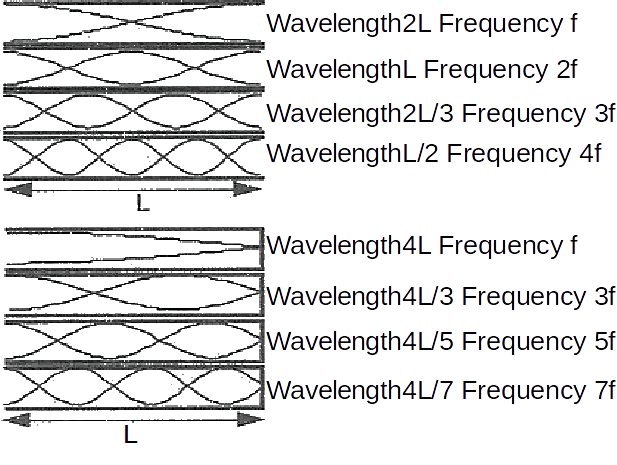
Transverse waves on a string
The ends of a string of length L, both of which are fixed, cannot oscillate. Traveling waves are reflected at both ends, so standing waves are possible. The only standing waves that fit the boundary conditions are those which have nodes at each end. The resonance mode with the lowest frequency f and longest wavelength 2L is called the fundamental, or fist harmonic. Higher frequency resonance modes are called harmonics or overtone. The second harmonic is the first overtone, the third harmonic is the second overtone and so on. The origin of these terms is musical. Stringed instruments produce notes in this way.

Longitudinal Sound Waves in a Pipe
A longitudinal standing wave can be produced in a pipe with open or closed ends. If an end of the pipe is closed the boundary conditions dictate that there is a node at that end, and if an end of the pipe is open, the boundary conditions dictate there must be an antinode at that end.