The crystalline stuture is said to form a lattice and may be investigated using x - rays. The bonds in crystalline materials tend to be metallic, ionic or covalent.
A lattice is "an infinite 1,2, or 3-D regular arrangement of points".
A 1D lattice could be polythene, which consists of the repeating unit - CH2 -
2-D patterns: Planar lattices eg graphit, which consists of laters of carbon atoms, each atom bonded covalently to three others, with weak forces between the layers.
3-D Space Lattices. There are 7 unique unit-cell shapes that can fill all 3-D space. These are the 7 Crystal systems.
We define the unit cell using 3 vectors,
\[\mathbf{a},\mathbf{b}, \mathbf{c}\]
called lattice paranmeters. The angles between these vectors are given by \[\alpha\]
(angle between \[\mathbf{a}\]
and \[\mathbf{c}\]
), \[\beta\]
(angle between \[\mathbf{a}\]
and \[\mathbf{c}\]
), and \[\gamma\]
(angle between \[\mathbf{a}\]
and {jatex options:inline}{\mathbf{b}/jatex} ).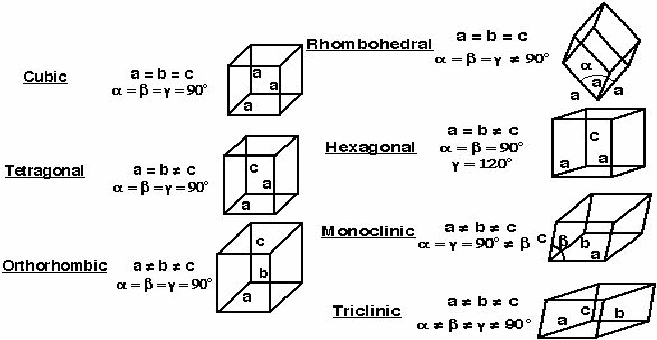 Although there are only 7 crystal systems or shapes, there are 14 different crystal lattices, called Bravais Lattices. (3 different cubic types, 2 different tetragonal types, 4 different orthorhombic types, 2 different monoclinic types, 1 rhombohedral, 1 hexagonal, 1 triclinic).
Although there are only 7 crystal systems or shapes, there are 14 different crystal lattices, called Bravais Lattices. (3 different cubic types, 2 different tetragonal types, 4 different orthorhombic types, 2 different monoclinic types, 1 rhombohedral, 1 hexagonal, 1 triclinic).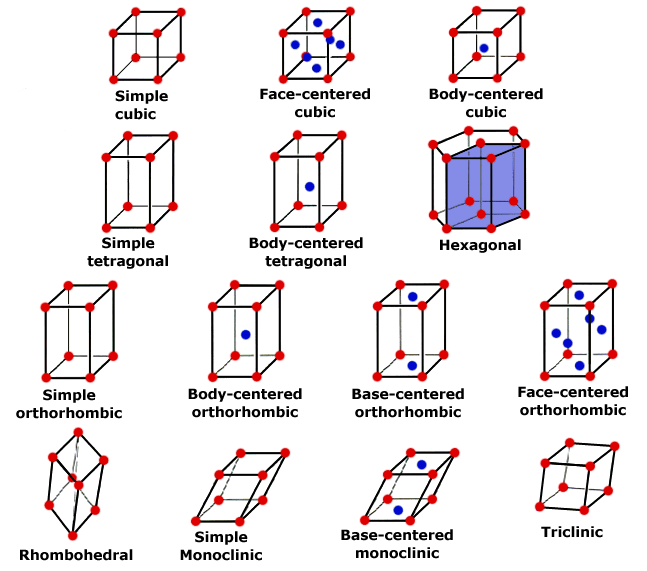
There are three types of cubic lattice.
The prmitive cubic has lattice points at the corner of a cube.
Body Centered Cubic (BCC) has lattice points at corners and centre of cube.
Face Centered Cubic (FCC) lattice points at the corners and centre of each face.
The lattice points at the corner of each cell are shared by the surrounding eight unit cells"worth 1/8 of a lattice point to each cell.
The lattice points at the centre of a face are shared between two cell so are only worth 1/2 a lattice point to each cell.
The lattice point at the centre of each cell belongs to that cell so contributes i1 lattice point to that cell.
Total number of lattice points i, for a primitive cubic 8(1/8) = 1, for a Face Centred Cubic 6x1/2 + 8(1/8) = 4, and for a Body Centred Cubic 8(1/8) + 1 = 2.
