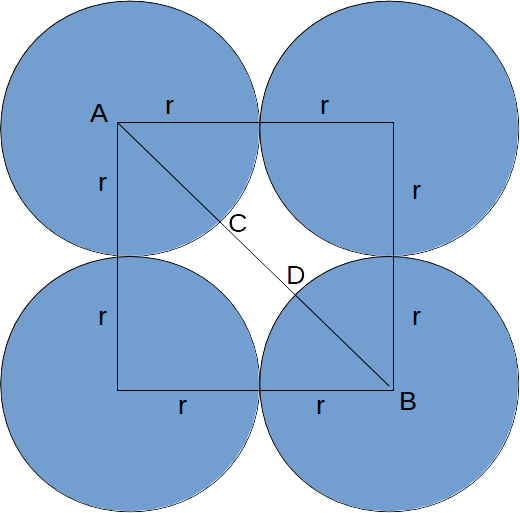
\[\sqrt{(2r)^2 + (2r)^2 } = 2r \sqrt{2}\]
The distance from C to D is then
\[\sqrt{(2r)^2 + (2r)^2 } -2r= 2r \sqrt{2} -2r\]
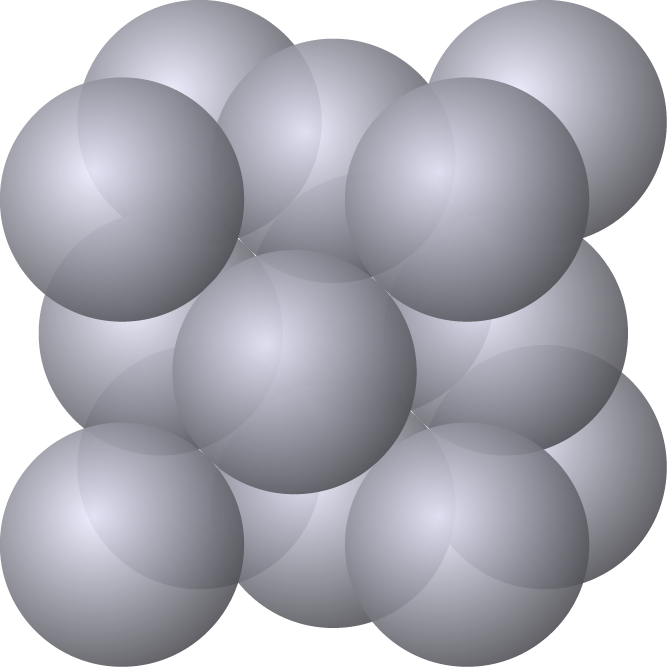
This face centred cubic structure has rotational symmety about the midpoint of AB, using the line AB as an axis of rotation, as well as vertical and horizontal rotational symmetry. This means that we can fit a sphere of radius
\[\frac{ 2r \sqrt{2} -2r}{2} = r (\sqrt{2} -1)\]
in this gap. 