Multiple Images may be formed by an arrangement of two or more mirrors.
Images Formed in Two Mirrors at Right Angles
When two mirrors are inclined at right angles we have not only the images
and
formed by single reflections but in addition two extra images formed by two reflections. The rays of light by which the eye sees one of these,
is shown in the diagram below left. The subscript
signifies the order in which reflection takes place from the mirrors 1 and 2.
The other image
may be seen by looking into mirror 1. Actually the images
andare superimposed on one another.
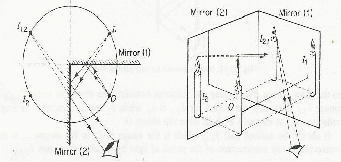
The images and act as objects for the formation of imagesandand the positions of these images are found in the usual way: a perpendicular to the mirror is drawn through the object and the object and image distances from the mirror are made equal.
Geometrically the object and the images all lie on a circle whose centre is at the intersection of the two mirrors.
More images may be formed by decreasing the angle between the mirrors. The they are inclined at an angle of 60 degrees, as in a kaleidoscope then six images are formed.
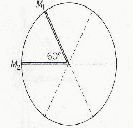
The object in a kaleidoscope consists of small pieces of brightly coloured glass, and looking through the tube at them, five images are seen, along with the original object. Every time the tube is shaken, the pieces of glass are rearranged and a different pattern is seen.
Image Formed By Two Parallel Mirrors
An infinite number of images are formed by an object placed between two parallel mirrors. These all lie on a straight line through the object perpendicular to the mirrors, illustrated below.
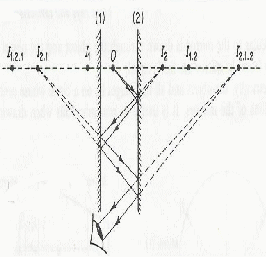
The position of of the images may be found by the usual construction, remembering that each image seen in one mirror will act as a virtual object and produce an image in the other mirror, so that the object for image
is image
The more remote the object, the more reflections and images there are and the fainter they become, since some light is absorbed by the mirrors with each reflection.