Any A Level student should know the values of any trigonometric function for any angle that is a multiple of 30 or 45 degrees. For convenience they are given below.
|
|
0 |
30 |
45 |
60 |
90 |
120 |
135 |
150 |
180 |
210 |
225 |
240 |
270 |
300 |
315 |
330 |
|
|
0 |
|
|
|
|
|
|
|
0 |
|
|
|
-1 |
|
|
|
|
|
1 |
|
|
|
0 |
|
|
|
-1 |
|
|
|
0 |
|
|
|
|
|
0 |
|
1 |
|
|
|
-1 |
|
0 |
|
1 |
|
|
|
-1 |
|
Using the values in the above table and the multiple angle formulae
and
We may find
and
for example if we choose the values of
and
properly. To find
we can choose
and
Then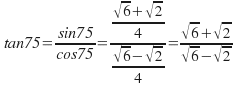
Now we follow the normal rules for rationalising the denominator. We multiply numerator and denominator by the conjugate root of the denominator. The conjugate root of
is
